The naivety of ML models and avoiding the naive trap
When machine learning models learn to be dumb.

Photo by pch.vector from Freepik.
The naive trap
You need a competitive edge when forecasting stock price movements. Therefore, you want your fancy machine learning (ML) models to learn something useful from the provided data that humans might not be aware of. This article will show you examples of where those fancy ML models learn something dumb that looks intelligent and how to check if your models are doing the same.
I came across this problem when comparing the stock forecasting performance of various ML models. After selecting the top-performing models, I made a quick comparison to a Naive benchmark model as a sanity check (the Naive model just uses the current price as a forecast for the next time step so it’s not an “intelligent” model that learns anything from historical data). After some investigation, I found that some of these ML models learned the Naive forecasting strategy, which left me with a couple of fancy-looking models that are no more useful than a toddler saying tomorrow’s price will be the same as today’s price. I fell into what I call the naive trap. Read on to learn how to avoid falling into the same trap.
It’s easy to fool yourself
Insidious confirmation bias creeps in fast as we spot the first signs of success in our beautiful money-printing ML creations and we forget to apply a rigorous scientific approach.
Most people get very excited to use ML. Using ML to solve problems is often romanticised (I’m also guilty here). There is a unique thrill accompanying the sight of a computer beating a human at some task: it simultaneously gives you a slight existential shake, making you wonder about your long-term relevance, while also satisfying your inner math geek and giving you a feeling similar to watching the first human landing on the moon. Because of this, we want our ML models to succeed. Insidious confirmation bias creeps in fast as we spot the first signs of success in our beautiful money-printing ML creations and we forget to apply a rigorous scientific approach. Consider the following example to see just how easy this can happen.
An example
Overview: setting the stage
In this example, I considered forecasting the next day’s price of Apple stock. I compared the performance of the following models (selected arbitrarily for illustration, feel free to plug in your own and rerun the analysis):
- Linear regression
- Random forest
- Multi-layer perceptron (MLP)
- Naive
A summary of the analysis is given below (the full analysis can be found in this GitHub repo).
Details: Data processing and setting the target variable
Firstly, the raw historical data was retrieved from Yahoo Finance. For data processing, some technical indicators were added as part of feature engineering. These features contain momentum, trend, volume, and volatility information and are commonly used as features in stock price forecasting. The data set features were also standardised so they were on a similar scale and appropriate for training ML models.
The data set was split into a training and a testing portion. As seen in the figure below, training was done on data from 2018–01–01 to 2021–05–31 (41 months) and testing was done on data from 2021–06–01 to 2021–12–01 (6 months).
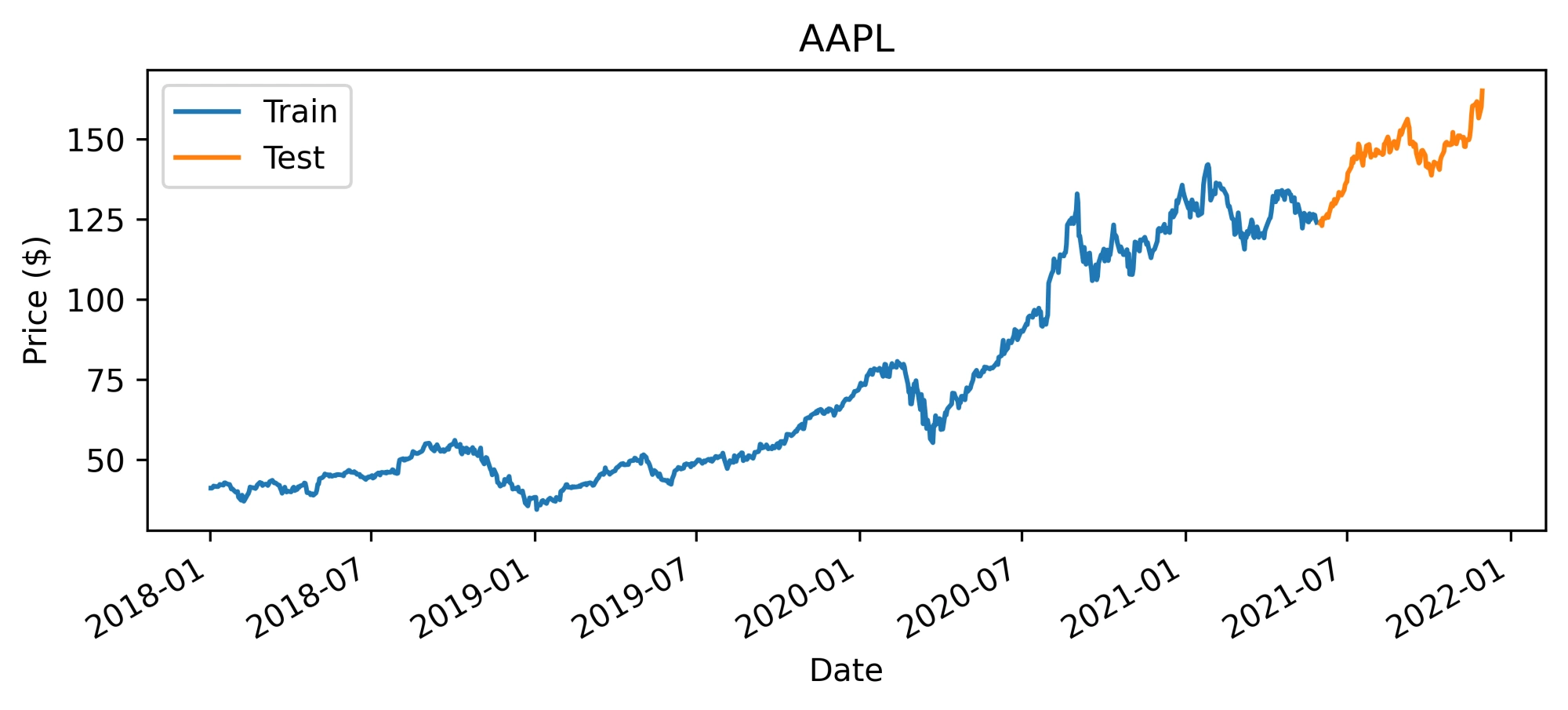
Price evolution of Apple stock during the train and test period (image by author)
In this supervised ML setting, the target was specified as the next day’s return. A price forecast can be reconstructed from the returns forecast. To do this, first, consider the definition of returns rₜ₊₁ at time t+1:
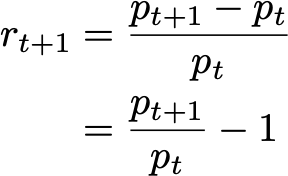
Where pₜ₊₁ is the price at time t+1 and pₜ is the price at time t. This can be rearranged to get an expression for the next day’s price:
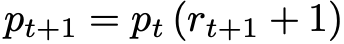
After training the above-mentioned ML models, their performance was assessed on the test set using the root mean squared error (RMSE):
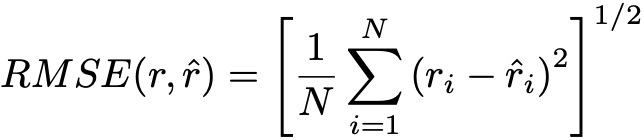
where r and r̂ are the actual and forecasted returns of the training set respectively, each containing N elements (the number of days in the test set). Because returns are used here, the result can be interpreted as a percentage price forecast error. The figure below shows the RMSE obtained by each model (lower is better).
Results: First appearances are deceiving

Root mean squared error (RMSE) of forecasts produced by models on the test set (image by author)
Notice that the errors of the Linear model and the Random Forest model are very close to that of the Naive model. At this point, you might be tempted to choose the Linear model as your top performer and happily put it into production, proudly claiming it makes just over a 1.2% error in price forecasts. However, when considering the strategy it learned to produce these forecasts, you might reconsider. Have a look at the following plot of return forecasts to see why this is the case.
Results: A closer look at what was learned
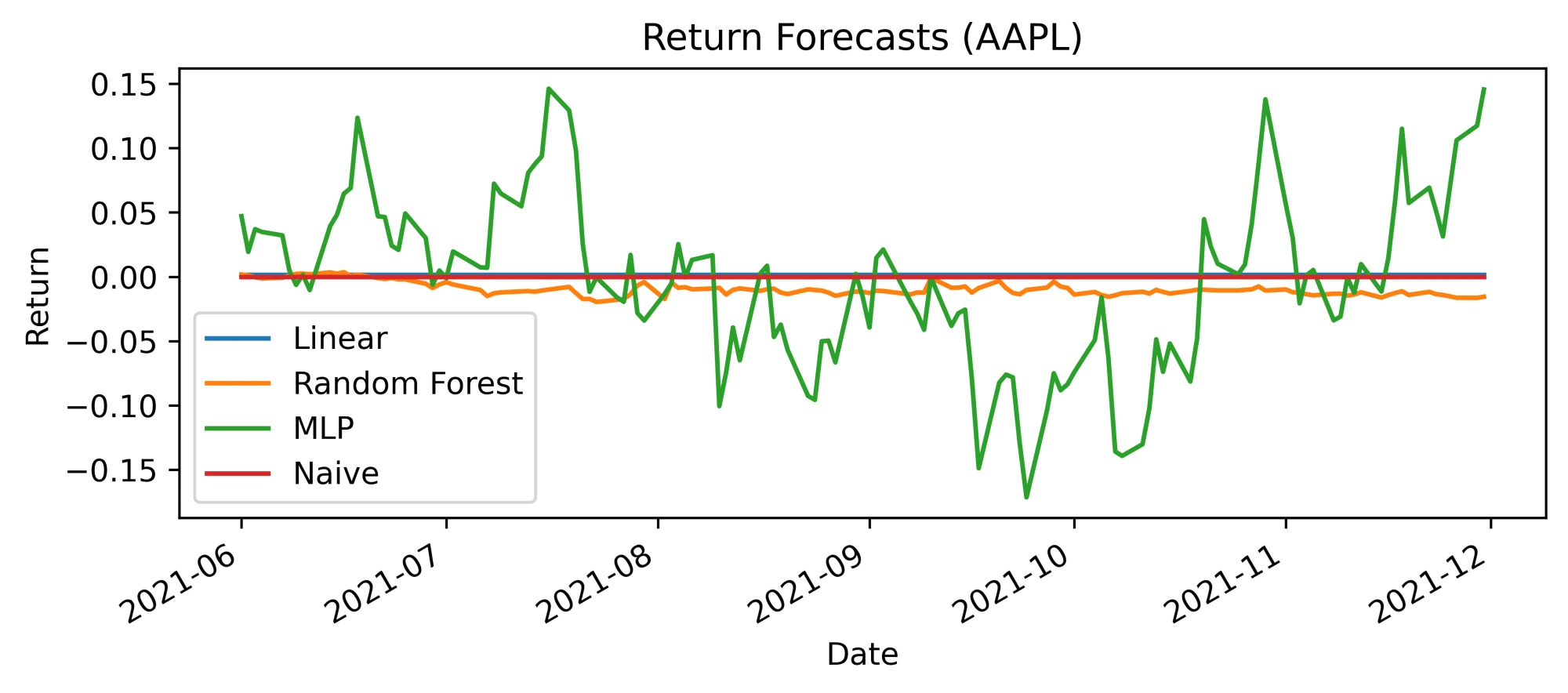
Return forecast produced by models on the test set (image by author)
A quick inspection reveals that the return forecast for the Linear model was almost always 0.0. This is the same as saying there will be no price difference between today’s price and tomorrow’s price. If this rings a bell, well done spotting it! This is of course the Naive forecasting strategy. It is also interesting to see the similarity between the Random Forest’s return forecast and the Naive model’s. Even though it is not as similar as the Linear model, it still very closely resembles the Naive strategy. These return forecasts can be converted into price forecasts as shown above to reveal a more intuitive and familiar plot:
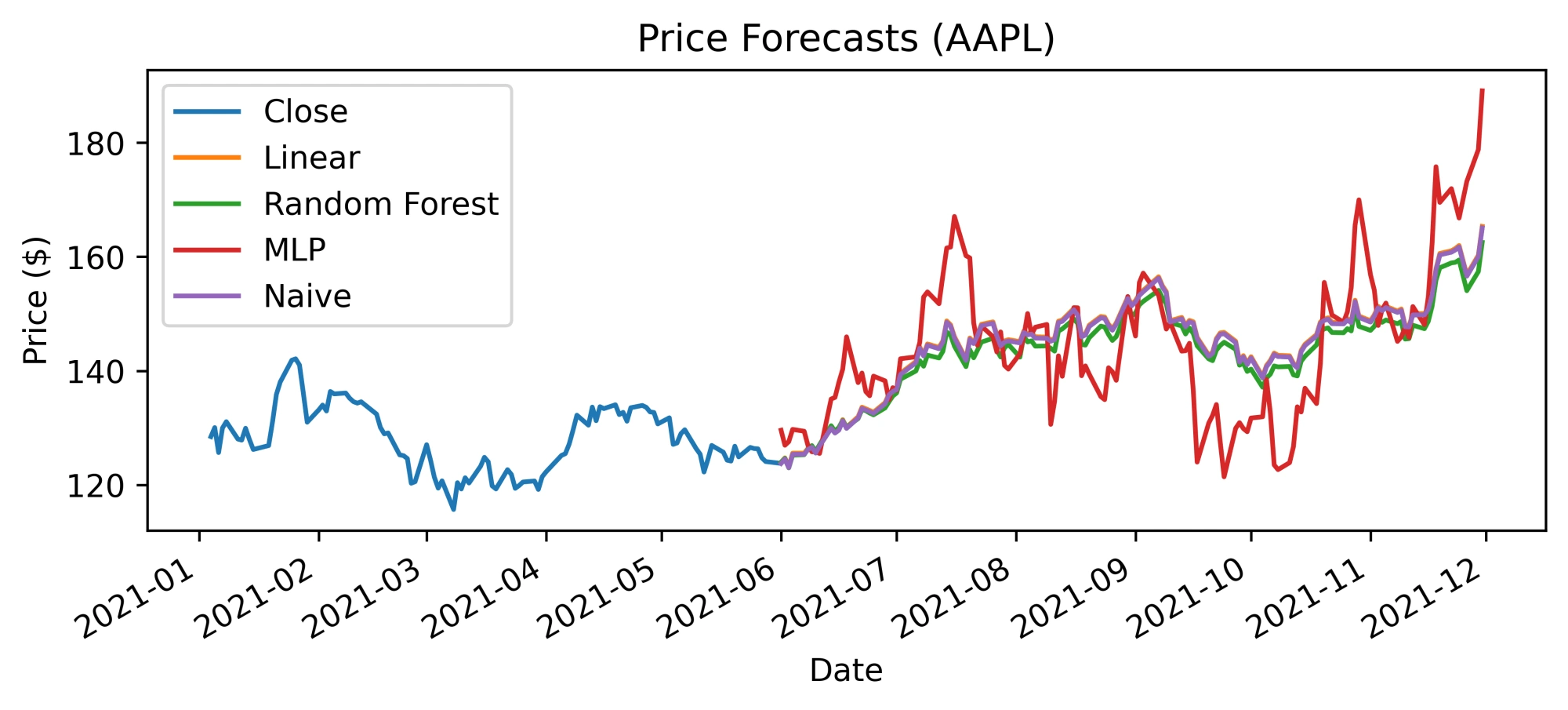
Price forecast produced by models on the test set. The close price is also shown (image by author)
This is a plot that more people will be familiar with. However, looking at this price forecast, it is not that obvious that the Linear and Random Forest models basically learned the Naive strategy. It is again easy to fall into the trap and conclude that the Linear model is a great solution.
A recipe for avoiding the naive trap
This is a great example of why data scientists shouldn’t blindly chase a technical metric to optimise. As you have seen, from that point of view, you can easily end up with “solutions” that are not very useful. Instead, consider the bigger picture when deciding what would constitute a solution to a given problem. This might mean further interrogating candidate solutions to see if they stand up to constraints not imposed by the original optimisation metric. In the case of stock price forecasting, consider adding the following steps to your process of finding a solution to avoid the naive trap:
- Have a look at the returns forecast
- Check how similar your ML models are to the Naive strategy (0.0 returns forecast)
- Consider eliminating Naive-like models from your list of top-performers
Conclusion
In conclusion, this article shows you how to avoid the trap of misinterpreting low price forecast errors and falling in love with your ML models before properly interrogating them. In the case of stock price forecasting, make sure that your complex ML models don’t learn something of little use like the Naive strategy after optimising for your preferred error metric. Simply plotting the return forecasts can give you valuable insight into this particular problem. Have a look at this GitHub repo for more details on the specifics of this analysis or to get you up and running with the same analysis quickly if you want to plug in your own models. Remember to always compare your ML models to simple benchmark models and happy forecasting!
Disclaimer: The information and content provided herein are meant for illustration purposes only. It is not intended for nor does it constitute financial, tax, investment, or other advice. Before making any decision or taking any action regarding your finances, you should consult a qualified Financial Adviser.
Resources
- Yahoo Finance for market data
- yfinance library for market data
- ta library for technical indicators
- scikit-learn library for ML models
- Republished here with permission from the original post on Medium
. . .